An input example for the pier like the figure 6 is below. It is 2.6 meters
high from the top of the beam to the position in the upper structure where
inertia force acts. This is the dynamic analysis which doesn't take the
basic spring into account, consider the footing bottom to be fixed, and
applies the type ll seismic movement 3 wave form to the direction of the
bridge axis. It has the M-φ element in the post foundation and the elastic
beam element in the middle part of the post.
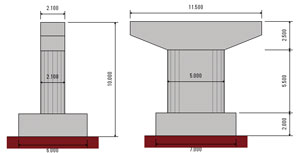 |
| Fig. 6 elliptical shaped pier (10 m high, 2 m thick in bottom) |
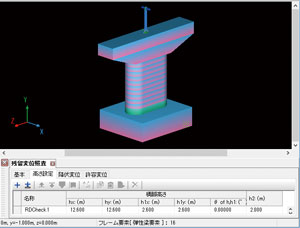
Case 1
This is an example of the modeling of the footing and that of the position
of the gravity center in the upper structure (Fig. 7). Mass 598t, which
corresponds to the shared weight of the upper structure, is in 2.6m high
above the top of the beam. The surround of the bridge axis of the spring
element that means the bearing is free at right angles in order not to
let the moment affect the top of the beam. In this case, the height would
be entered as "h=12.6m, h1=2.6m, h2=2m". Yield displacement would
be 41mm in 2.6m above the top of the beam.
Case 2
This is the modeling without the footing and the upper structure position
like the figure 8. Mass 598t, which corresponds to the shared weight of
the upper structure, is located at the top of the beam. The height would
be entered as "h=8m, h1=0m, h2=0m", and the yield displacement
would be 23mm at the top of the beam.
 |
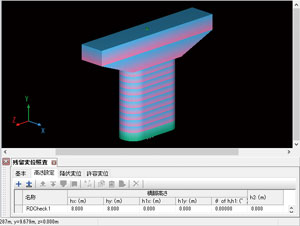 |
 Fig. 7 With the footing and the gravity center position Fig. 7 With the footing and the gravity center position
of the upper structure |
 Fig. 8 Without the footing and the gravity center position Fig. 8 Without the footing and the gravity center position
of the upper structure |
|

