|
Overview
The following functions have been added to Engineer's Studio® Ver.10.
- M-φ element that takes into account the influence of change in axial force
- M-θ model (spring element) that takes into account the influence of change in axial force
Both functions can be applied to uniaxial bending but not to biaxial bending. Use the fiber element for the biaxial bending
M-φ element that takes into account the influence of change in axial force
As for M-φ characteristics automatically created from sections, input the maximum and minimum value and the number of changing axial force in the M-φ Tables or M-φ Thumbnails in "Model Properties | M-φ Element Properties". Then press "Preprocess" button to calculate the same number of M-φ characteristics as the input number of axial force (Fig.1).
To calculate arbitrary M-φ feature that is not calculated from section automatically, input M and φ the same number as axial force directly.
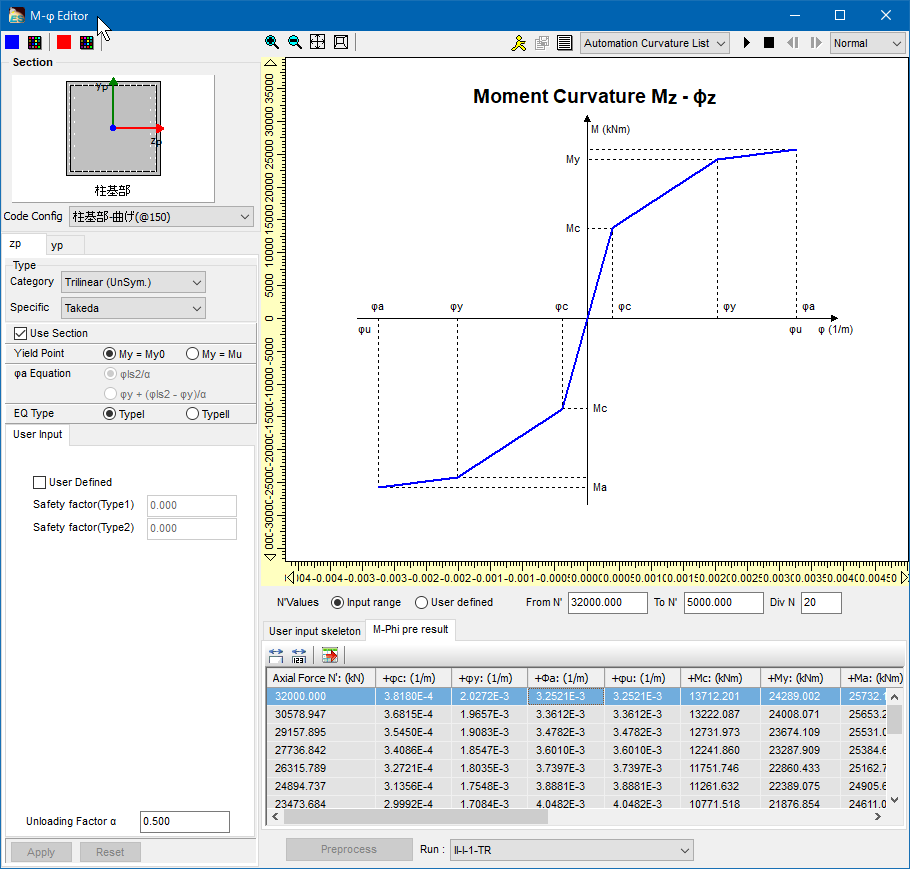 |
| Fig.1 M-φ feature that takes into account the influence of change in axial force |
When the FEM analysis is performed, M-φ features of each axial force are taken into account at the same time. The figure 2 is an example of an analysis of the case of 3 axial forces. M-φ characteristics when the axial force is N1, N2, and N3 are available.
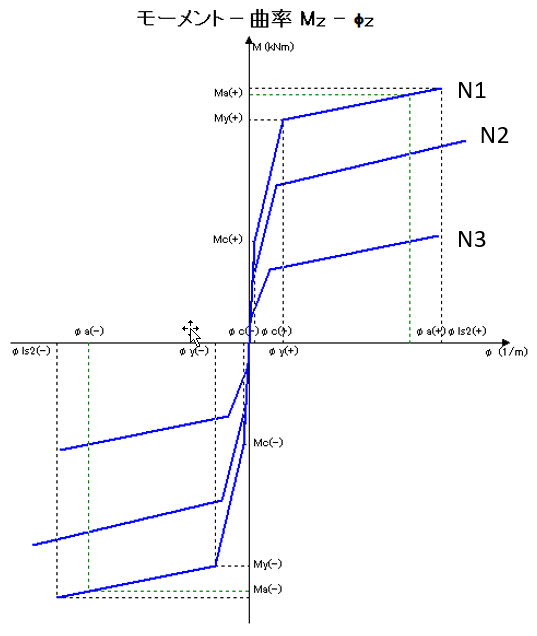 |
Fig.2 Moment Curvature Mx-φz
Example of several M-φ characteristics according to 3 types of axial forces |
When a load is applied, in a step, all the three M-φ characteristics are updated at the same time as shown in Fig. 3 and reach the point A, B, and C. For example, when a new axial force acquired at that step is between N1 and N2, the linear interpolation is applied between A and B and creates a new bending moment and rigidity.
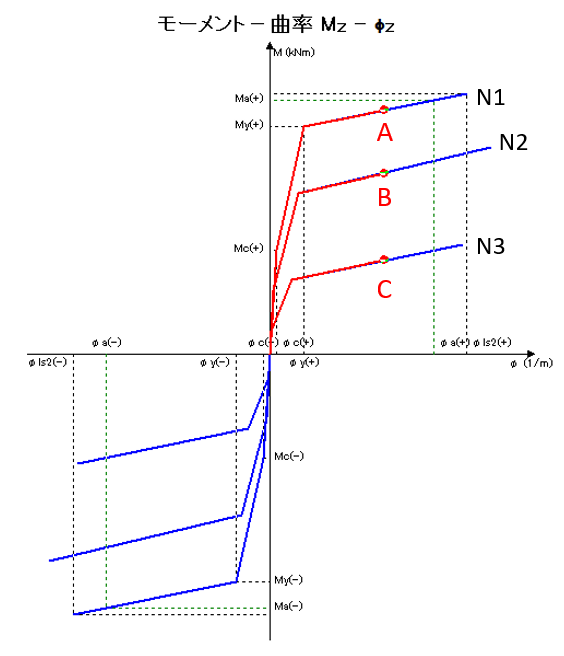 |
Fig.3 Moment Curvature Mx-φz
Response of several M-φ characteristics when monotonically increasing |
The unloading is handled in the same way. In a step, all the three M-φ characteristics are updated coinsidently as shown in Fig. 4 and reach the point D, E, and F. For instance, when a new axial force acquired at that step is between N1 and N2, the linear interpolation is applied between D and E and creates a new bending moment and rigidity.
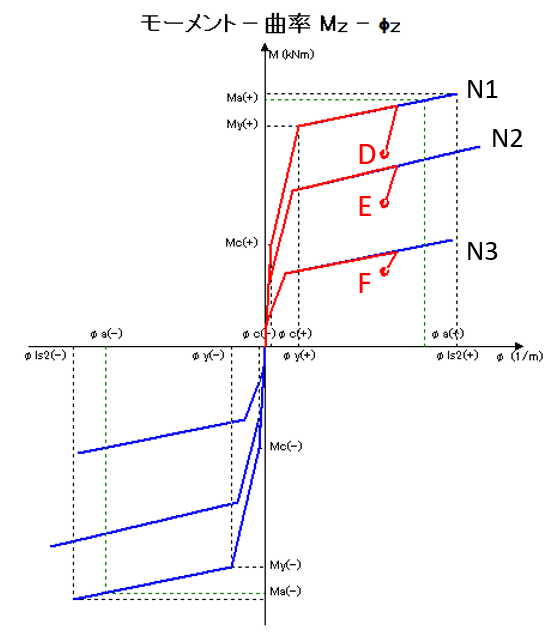 |
Fig.4 Moment Curvature Mx-φz
Response of several M-φ characteristics when unloading |
M-θ Model (Spring Element) That Takes Into Account the Influence of Change in Axial Force
Handled in the same way as M-φ element above that is taking into account changes in the axial force.
Others
Response value and verification value that take into account changes in the axial force is also calculated for the curvature verification, plasticity rate verification (2012 specifications), residual displacement verification, and displacement verification (2017 specifications).
|