|
「西日本構造解析研究会」における退官記念講演会
幾何学的非線形構造解析法における有限要素法の功罪
佐賀大学 後藤茂男
1.まえがき
わが国における構造解析の分野に、有限要素法が取り入れられるようになってすでに久しいが、土木工学の分野では、それ以前、すでに骨組構造に対しては、たわみ角法を起源とした変位法(当時は変形法と呼ばれていた)が定着しており、当時の計算センター各社の大型計算機の利用を前提としたマトリックス構造解析法のプログラムの開発も盛んに行われていた。
しかしながら、有限要素法が本来の連続体のみでなく骨組構造を含めた有限要素構造全体に対する汎用理論として喧伝され普及するに従い、微小変位理論のはり要素に対してさえ、初等構造力学における断面力の概念と部材座標系における独立な部材力式からの座標変換による共通座標系に関する剛性方程式の定式化という既得の知識の延長としての身近な変形法の手法に代わり、ひずみと変位の関係式と要素内変位の多項式による補間から説き起こす有限要素法の手法を用いる参考書なども一般的なものとなってきた。
さらに、幾何学的非線形解析においては、その傾向は加速され、要素内でのひずみと変位の関係式として非線形項を付加した
Green-Lagrange のひずみテンソルを用いる有限要素法の拡張理論が一般的な手法として位置づけられ、土木工学ハンドブックや有限要素法ハンドブックなどにも採りり上げられている。
このように有限要素法が、骨組構造も含めての汎用理論として位置づけされたのとは逆に、土木工学で定着していた変形法を有限要素構造に対する汎用理論へと発展させることも可能であり、またその方が現在の難解すぎる幾何学的非線形解析法の輩出もなく、より簡明で実用的かつ高精度な汎用解析理論への展開と普及が容易ではなかったかと考えられる。
本論文は、これらの根拠と一般的な有限要素法による幾何学的非線形解析法の問題点を、変形法の拡張理論として筆者らが提唱してきた要素剛性分離の手法による接線剛性法と対応させながら考察、検証するものである。
2.要素剛性分離の手法による接線剛性方程式と接線剛性法の汎用性
接線剛性法のための要素剛性分離の手法と有限要素法の比較の論拠の基本を明確にするため、周知の変形法の理論を示しておくことにする。
有限要素構造物を構成する単一要素を取り出し、これに静定で安定な支点拘束条件を設定し、無拘束方向の節点力と対応する変位の組み合わせを要素力と要素変形と定義し(要素座標系の設定)、その関係式を要素力式あるいは要素力剛性方程式と呼ぶことにする。

この必要最少限の要素力式は、要素内荷重が作用しない場合の要素の可能な応力・ひずみ状態を表し得るものである.
要素には、他の要素と連結して全体構造系を構成するための複数の節点(要素端)があり、それらの節点に作用する共通座標系方向の節点力と要素力との関係を求める。
平衡条件式 U=αS …………………………………………………………………………
(2)
U:要素端における作用力の共通座標系方向の成分によるベクトル
α:要素力を要素端節点力へと変換する要素座標系の共通座標系に関する方向余
弦等から構成されるマトリックス
Uに対応する節点変位ベクトルuと要素変形ベクトルの関係式すなわち適合条件式はαの転置マトリックスを用いて
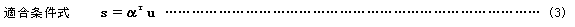
となることから、共通座標系に関する要素の節点力と節点変位との関係すなわち剛性方程式が次式のように得られる。

すなわち、これを全要素について適用し、重ね合わせることによって全体構造系の剛性方程式が得られることになる。
有限要素法では、応力・ひずみ関係からひずみと変位の適合条件、変位関数の設定と要素内積分を用いて、要素力式、平衡条件式を経由せずに直接剛性方程式が導かれる場合が多く、変形法でも直接、共通座標系に関する剛性方程式を示す教科書もあるが、ここでは要素力と要素変形の設定という過程を省略しないことがきわめて重要である。
以上の式(1)から(4)に至る変位法の拡張理論としての接線剛性法のための要素剛性分離の手法では、式(2)を先行状態における平衡条件式とすることから出発する。
先行平衡状態からの変動を考えるために、式(2)を微分すれば
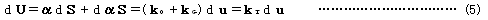
となり、中辺第1項は要素力剛性に関する接線剛性マトリックス、第2項は接線幾何剛性マトリックスを導き
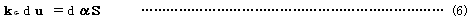
あるいは、微小増分記号dに対して有限増分記号⊿を用い、先行状態における要素力Sを一定として
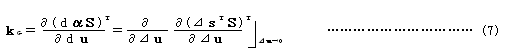
が成立する。 ここで式(5)からの全体構造系に関する接線剛性方程式を
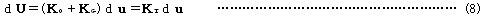
として、接線剛性法は、初期平衡状態の荷重ベクトルU=U0
に新たに付加する荷重ベクトル⊿Uを初期不平衡力として荷重項dUと置き、以下の過程をたどることになる。
- dUを与えて全体構造系に対する接線剛性方程式を解き得られた変位増分より変位⊿u=⊿u+du を求める。
- 全節点の座標値、回転量などを修正し、厳密な適合条件を用いて要素変形を算出する。
- 要素変形から設定した要素力式に忠実に要素力を求め、共通座標系に関する要素の新しい変形状態に従って作用する要素端力の合力として全節点の作用節点力U1を求める。
- 以上の状態の構造系と作用節点力U1を新たな先行状態として不平衡力
dU=U+⊿U-U1 を求める。
- 不平衡力の最大値が許容値以上の場合、新たな先行状態における座標値、要素力を用いて接線剛性マトリックスを求め1)以下の過程を反復する。
すなわち、この反復過程は次式によって表すことができる。
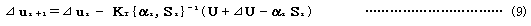
また、次の図-0 は、接線剛性法の反復概念を表すものであり、これにより本反復手法の収束過程を説明すれば以下のようになる。
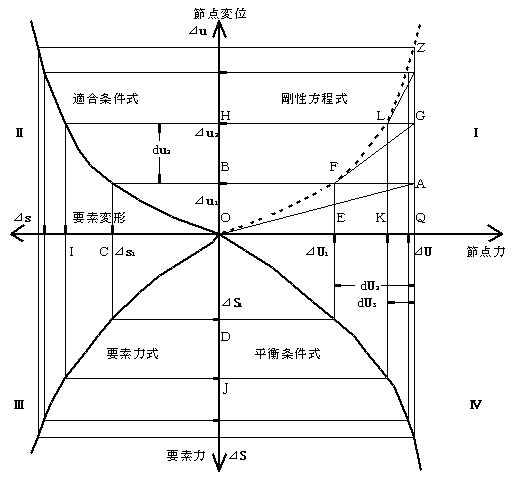
図-0 接線剛性法の収束概念図
第1象限における変位と荷重の厳密な関係を表す非線形の剛性方程式は、本手法では与えられておらず、ここでは点線で示しておく。
第2象限は共通座標系に関する節点変位⊿uより各要素固有の要素座標系に関する要素変形⊿sを求める適合条件式、第3象限は要素変形から対応する要素力⊿Sを求める要素力式、さらに第4象限は各節点に集まる要素の要素力から変形後の形状を考慮した座標変換により算出される節点力としての荷重を求める平衡条件式を表すものとする。
原点 O は既知の平衡状態で、接線剛性法の反復手法は、まず与えられた荷重増分としての節点力⊿U(Qで示す)に対してO点を先行状態とする接線剛性方程式を解き⊿u1を得る(O→A→B)。
この変位⊿u1 に対して適合条件式により要素変形⊿s1、次に要素力式により要素力⊿S1さらに平衡条件式を用いて、その変位状態を発生せしめる厳密な荷重状態としての⊿U1を計算することにより(B→C→D→E)新しい平衡状態Fを設定する事ができる。
もちろん、この状態はまだ目的の状態とは異なり、与えられた荷重⊿U に対してdU2=⊿U-⊿U1
:(Q-E)の不平衡力が存在する。 したがって、この状態Fを先行状態とする接線剛性方程式(F→G)を用いてdU2に対する解du2
:(H-B)を求め、新しい変位 ⊿u2 =⊿u1+du2 よりH→I→J→Kとして⊿u2を満足せしめる荷重状態Kが得られ、次の先行状態としてLの設定が可能となる。
したがって、この状態 Fを先行状態とする接線剛性方程式(F→G)を用いてdU2に対する解du2
:(H-B)を求め、新しい変位 ⊿u2 =⊿u1+du2 よりH→I→J→Kとして⊿u2を満足せしめる荷重状態Kが得られ、次の先行状態としてLの設定が可能となる.
以下これを反復することにより、O→F→L…→Z と無限にZに近づけることができる.
要するに接線剛性法は、力学的に簡明な接線剛性方程式の定式化に加え、非線形の剛性方程式を使用しない数学的には
Newton-Raphson 法と等価な反復手法であり、接線剛性方程式の定式過程と整合する要素変形、要素力の算出など、1)~5)に示した手順が一体となってその効果を発揮するものであり、剛体変位を拘束された単体の構造系としての全挙動を規定する要素力式に従う要素によって構成された全体構造系の厳密解を与える。
したがって、構造物の変形挙動の真の解としての曲線形状と、接線剛性法による収束解による形状との差は、たとえば平面骨組み構造の場合、要素力式に通常のはり、柱の微分方程式の解を用いた場合には、節点間の真の曲線形状を両端の位置と回転を一致させて要素力式の解が取り得る解析曲線で近似させた場合の曲線長の比と1との差が誤差の目安となることが確かめられている。
また、変位制御による解析においても、強制変位を与える節点に、その変位の方向のみを拘束する支点条件を与え、まず、1)において、剛性方程式は解かずに拘束方向の変位のみを所定の変位量とし他は0としたものを変位ベクトルとして
2) 以降の手順をたどればよく剛性マトリックスには、支点条件のほか特別な操作を加える必要はない。
さらに、反復に際しての初期近似値の設定とか、付加荷重が大きすぎるための分割増分毎の載荷とかの必要はなく、無応力状態からいわゆる弾性座屈近傍の不安定領域となるような荷重増分を一括載荷しても解が存在すればその解へ、また複数の解がある場合にはいづれかの解へ確実に収束する。
ここで示した接線剛性法の平衡条件式(2) 以降の理論展開は、要素の節点の個数とその種類(剛節か滑節か)によって統一され、直線棒要素とか、曲面シェル要素あるいは立体ブロック要素といった、要素自体の種類とは完全に無関係となり、構造物の幾何学的非線形解析にとって最重要な要素変形と節点変位の適合条件の非線形性に起因する厳密な接線幾何剛性を統一的に定式化し得る。
たとえば、4節点剛節4面体要素と4節点剛節曲面シェル要素も全く同一の接線幾何剛性として定式化することができ、これらのことからも変形法の延長にある本手法が、有限要素法以上に骨組構造に限定されない、有限要素構造における幾何学的非線形解析の汎用理論としてきわめて有用であることが理解されよう。
なお、以上のような接線剛性法的分類によりモデル化された有限要素の要素力式は、一般的には、既述のように要素に静定で安定な支点条件を設定、その要素に固定された要素座標系に関する無拘束方向の節点力とその対応変位の組合わせ、立体多節点滑節要素の場合には、全節点を連結する内的に静定な仮想トラス骨組を想定し、その部材力と部材の伸縮量との組合わせなど、要素内の応力・ひずみ状態を定める剛体変位に影響されない要素力と要素変形間の関係式として、各要素の種類に応じた理論による定式化として研究されることとなり、連続体からの有限要素モデルなど、ここで本来の有限要素法の理論が展開されるところであろう。
このように、要素力式は、最も効果的に剛体変位を除去しての選定が可能なため、要素分割が適当であれば、微小変位理論を用いても実用上十分な精度の解が得られ、また分割をさらに密にすることにより誤差を激減させることが可能である。
さらに特筆すべきことは、本手法における接線幾何剛性は、要素剛性から完全に分離独立して存在するものであり、このことから、要素剛性を持たず幾何剛性のみの要素からなる構造系を想定する事により、2次元幾何剛性要素、あるいは四面体幾何剛性要素による石鹸膜構造系、1次元幾何剛性要素による軸力線構造など、分布張力や軸方向力のみの釣り合い系の解析も可能となり、大空間膜構造や曲線格子ドームの形状決定解析にも適用し得るということである。
3.有限要素法による直線棒要素の幾何剛性マトリックス
有限要素法による幾何学的非線形解析理論に関しては、数多くの研究がなされており、これらを総括して論じることは不可能であるが、海外において、多くの研究者が解析理論の展開の基礎とし、いわば正統的と見なされ、わが国でも土木工学ハンドブックや有限要素法ハンドブックなどにも示されている理論を用いた直線棒要素の幾何剛性マトリックスの定式化について考える。
一般的には有限要素内でのひずみと変位の関係式を非線形項を付加した Green-Lagrange
のひずみテンソルで設定、要素内の応力や変位を多項式で補間し、仮想内部仕事の要素内積分により接線剛性マトリックスkTを導く。
kTはひずみテンソルの非線形項に起因する幾何剛性マトリックスkGと微小変位理論としてのマトリックスk0の和として表示されるが、一般にkTおよびkGは陽な形で厳密に表すことはできない。

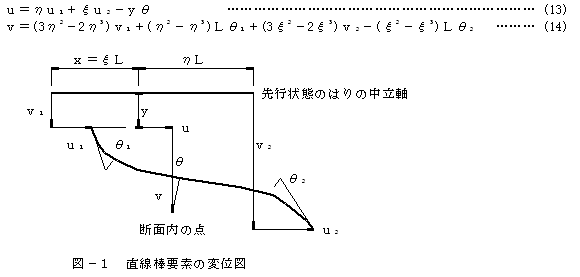
直線棒要素に関しては、図-1に示すような、変位前の要素の状態を水平として、断面内の着目点の変位は、中立軸の水平変位を1次関数、垂直変位を3次関数と仮定すれば次式が得られる。
軸方向ひずみと変位は、有限変位のひずみテンソルより
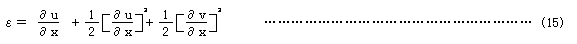
となるが、右辺第2項は、その微小性と垂直変位がない場合のはりの軸方向変位との整合性から省略される場合も多い。すなわち、εを線形ひずみεLと非線形ひずみεNにわけて次式を用いる。
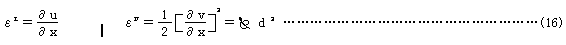
したがって、非線形ひずみは、垂直変位の変位勾配dによってのみ表示されることになる。
ここで、変位勾配は
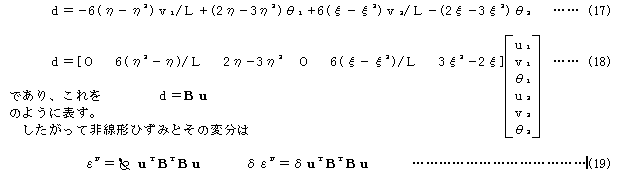
となる。
線形ひずみによる仮想仕事式は微小変位理論による剛性マトリックスを、非線形ひずみと先行状態における応力σ0による仮想仕事式は接線幾何剛性マトリックスkGを導くことになり
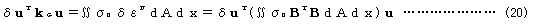
が成立する。
先行状態における応力σ0は曲げモーメントをM、軸方向力をNとすれば
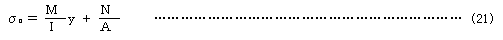
であり、二重積分において,断面内、中立軸に関する積分 ∫dA=A、∫ydA=0 を考え

として接線幾何剛性マトリックスを求めることができる。
BTBは、6行6列の対称マトリックスであり、そのij要素をBijとして、その非零要素を求めれば次のようになる。
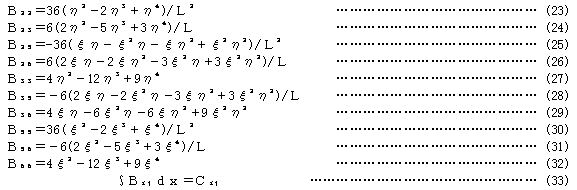


4.接線剛性法のための要素剛性分離の手法による2節点要素の接線幾何剛性マトリックス
有限要素法との比較・考察のため、要素剛性分離の手法による2節点要素の接線剛性方程式について考える。この場合の接線幾何剛性マトリックスは力の釣合と適合条件の幾何学的考察のみからでも容易に定式化できることに注目されたい。 接線剛性法では、まず要素内の応力とひずみの分布状態を規定することのできる要素端(接続節点)に関する独立な要素端力と対応する変位の組合わせを要素力と要素変形として設定しなければならない。すなわち、要素に静定で安定な支点条件を考え、支点反力を除く節点力とそれに対応する節点変位の組み合わせであり、2節点要素の場合、図-2のように要素座標系として
(b)単純ばり座標系と(C)片持ちばり座標系による組み合わせが考えられる。
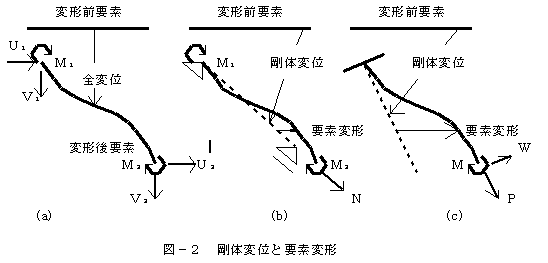
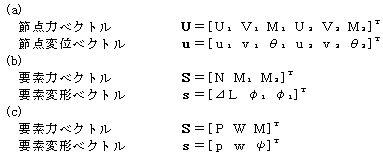
しかしながら、(b)を用いた場合には、その収束解の精度が要素分割数を2倍にした(c)の場合と同等となり、明らかに(c)より有利である。
したがって、ここでは、単純ばり座標系を採用することにする。
前述のように本手法によれば、要素は、通常の有限要素法の手法による場合のように直線である必要もなく、平面2節点要素であれば何でもよい。
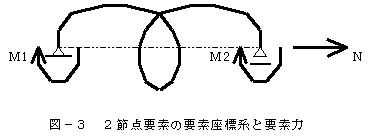
すなわち、要素力ベクトルを
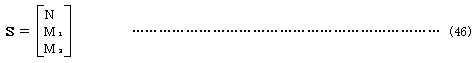
として、要素の共通座標系に関する、要素端の節点力への変換式(平衡条件式)を求める。
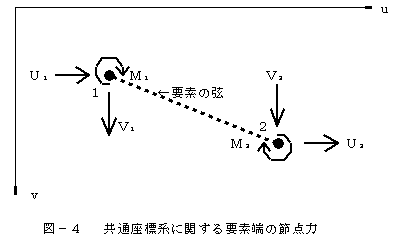
弦長をL、共通座標系に関する弦1→2の方向余弦をα、βとすれば
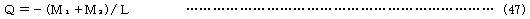
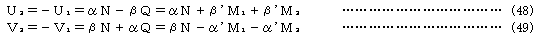
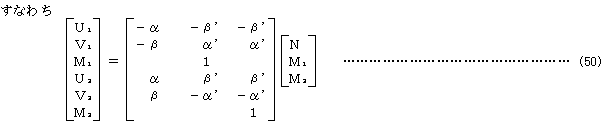
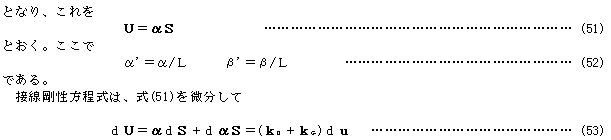
のように表され、中辺第1項は要素力剛性に関する接線剛性マトリックス、第2項は接線幾何剛性マトリックスを導く。
共通座標系に関する弦長の水平成分をx、垂直成分をyとすれば
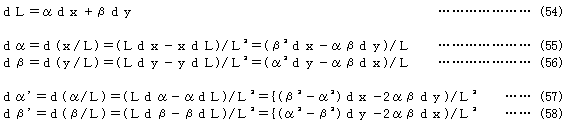
となり、したがって μ=N/L ν=Q/L とおいて
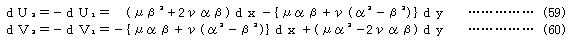
が得られる。また、要素端の並進変位の微分量と弦の投影成分の変化との関係は
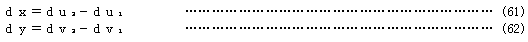
である。以上により、dUに対応する要素端の節点変位の増分duに対する接線幾何剛性マトリックスが次のように得られる。
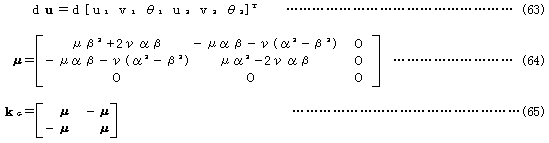
5.変形法の延長理論としての簡単な幾何学的考察によって得られる2節点要素の幾何剛性
上記の接線幾何剛性マトリックスは、また以下のような簡単な考察によっても容易に導くことができる。 変形後の2節点要素を平行移動して一端を変形前と一致させ他端の弦方向およびその直角方向の要素端力、および共通座標系に関する要素端変位を図のように定める。
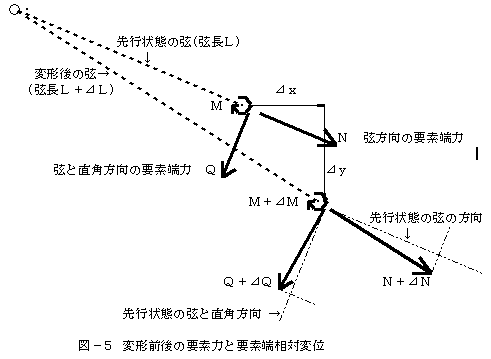
変形後における要素力において、先行状態ですでに先行荷重と釣り合っていた成分を除去して、新たな荷重増分と釣り合うべき共通座標系方向の成分の簡単な幾何学的考察により、剛性方程式における最も重要な幾何剛性部分を定式化する。
α、βを水平および垂直座標軸に対する先行状態の弦の方向余弦とすれば、2次以上の変位を省略して
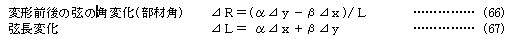
が成立する。
変形後における要素端において、新たに釣合を考慮すべき変形前の弦方向およびその直角方向の成分は、すでに釣合っているN,Qを差し引いて
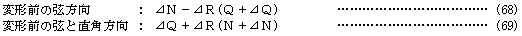
となり、⊿Nはそのまま、弦長変化に対する要素力式により要素力剛性を表す項へと変換されるが、⊿Qは端モーメントM(両端のモーメントを代表させる)の関数となるので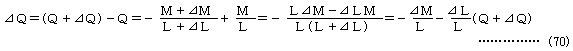
のように、曲げに関する要素力式と幾何剛性部分に変換される。
したがって、変形前の弦方向およびその直角方向の成分における、要素力増分⊿N、⊿Mに関する項を除いた先行要素力を含む幾何剛性項を⊿NG、⊿QG とおけば
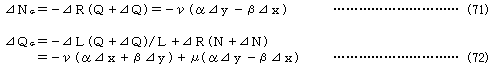
となり、共通座標系の要素端力増分において要素力剛性部分を除いた幾何剛性に関与する項は
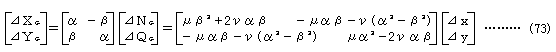
のように表される。ここに、μ、νは以下のように置いたものである。
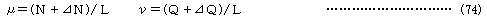
すなわち、係数マトリックスは、接線幾何剛性としては、上式において⊿N、⊿Qを省略すればよく、結局、式(64)と全く同じものが得られたことになる。
μ、νの中の⊿N、⊿Qを非線形項として、単純な反復計算により解を求める手法もあり、大部分の構造解析において、実用上は、十分な精度の解が得られ、これは吊橋の弾性理論に対するたわみ理論の活荷重水平力⊿Hを反復代入して解を得る手法に相当する。
6.両理論による幾何剛性マトリックスの比較と考察

と接線剛性法のための要素剛性分離の手法により得られた式(65)との比較のため先行状態の要素の弦を水平とする。 すなわち α=1 β=0 とすればと接線剛性法のための要素剛性分離の手法により得られた式(65)との比較のため先行状態の要素の弦を水平とする。
すなわち α=1 β=0 とすれば
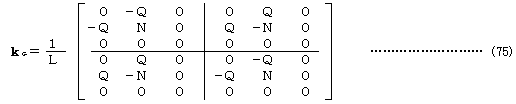
となり、この方が単純ではあるが、式(45)にはないせん断力の項が存在する。
接線剛性法方程式

において、接線剛性法と有限要素法における顕著な相違点は

である。すなわち、接線剛性法におけるkGは要素の種類には全く無関係であり2節点要素という制約以外には拘束されないきわめて汎用性のあるものでり、当然、要素力式における非線形性はk0中含まれる。 したがって、両者を対等の条件で比較するためには、要素を直線棒部材に限定して、その要素力式(部材力式)の非線形性に起因するk0中の幾何剛性をkGに加えてやる必要がある。 先行状態における簡単な接線要素力式として
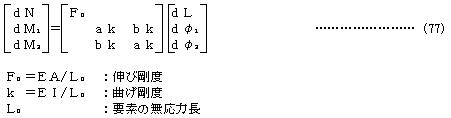
を用い、双曲線関数または三角関数となるa、bを級数展開してNの2次以上の項を省略すれば

とおいて、これの幾何剛性項を接線剛性法のkGに加えkGとすれば次式が得られる。
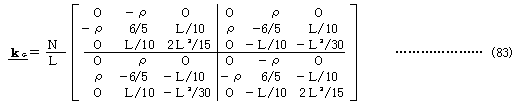
式(45),(66),(74)を比較することにより、有限要素法の幾何剛性マトリックスに含まれる本来要素力剛性に起因する部分は次式で表されることがわかる。
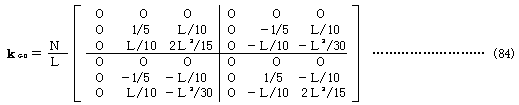
しかしながら、これらは、要素の細分化により急激にその影響が減少するものであり、残りの部分の要素の細分化に左右されない、構造解析における本質的な幾何学的非線形効果を表すマトリックスは
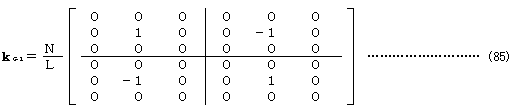
のように、きわめて単純なものであり、最初から要素剛性を分離した、簡明な定式化による接線剛性法などの場合と比べれば、ここでせん断力による項が欠落していることがわかる。
また、kG0も、最も単純な軸方向力を受ける単純ばりの解からの幾何剛性成分と等価であり、有限要素法では、必ずしも厳密とは言えない両者が混交して、直線棒部材として限定された構造要素専用の幾何剛性マトリックスを構成していることになる。
要するに、このような一般的な有限要素法の手法による、ひずみテンソルの非線形項からの幾何剛性項の定式化においては、さらに厳密な考察によって高精度化を目指しても、それは、要素の細分化により、その影響が激減する剛体変位を拘束された要素の挙動を記述する要素力式を補完しようとすることに他ならない。
7.接線剛性法による計算例と幾何剛性項Q/Lの省略が解の収束性に及ぼす影響
ここでは、接線剛性法の高精度、高収束性かつ使い易さを示すための計算例と、ハンドブック等に示されている式(45)
に見られるQ/Lの省略が、解の収束性に及ぼす影響を接線剛性法の手法により確認する。 |